tg-me.com/knowledge_accumulator/251
Last Update:
Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning - венец творения ML в играх
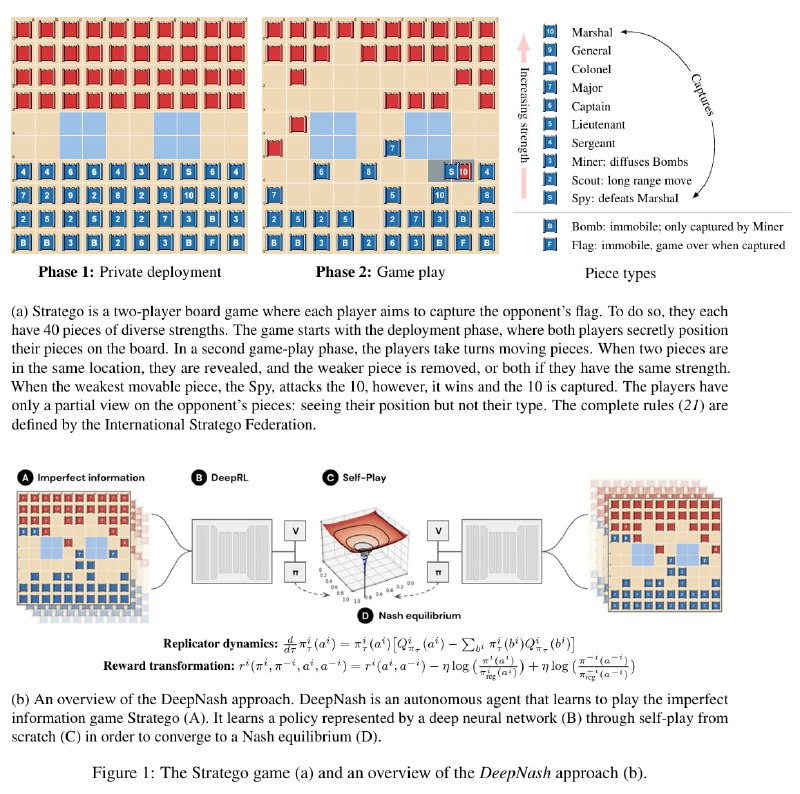
AlphaZero - это, конечно, хорошо, но есть проблема - Го и тем более шахматы - простые настольные игры с полной информацией. Авторы данного исследования решили покорить игру Stratego - в 10^175 раз большую игру, чем Го, и при этом с неполной информацией. На первой половине картинки можно почитать правила - сначала игроки в закрытую расставляют 12 видов фигур на поле, а затем ими ходят.
Я не большой специалист в теории игр, и глубоко осознать происходящее в статье мне не под силу. Однако, на выходных мне удалось пообщаться с анонимным экспертом по равновесию Нэша и разузнать кое-какие детали.
Итак, в ~любой игре из, скажем, 2 игроков, существует пространство пар стратегий, находящихся в равновесии - они являются максимально сильными по отношению друг к другу, и ни одну из них нельзя улучшить так, чтобы увеличить её среднюю награду. Для простоты буду называть любую из таких стратегий Нэш-оптимальной.
Смысл жизни ресёрчера в сфере игр - поиск алгоритма, строящего Нэш-оптимальную стратегию для любой игры. Результатом теоретического анализа последних лет стал алгоритм, позволяющий в играх с неполной информацией гененировать Нэш-оптимальную стратегию "разумным" образом, и он довольно близок к тому, что можно увидеть в RL. Он состоит из 3 основных блоков, повторяющихся по кругу:
1) Self-play
2) Пересчёт награды со специальным регуляризатором, позволяющий алгоритму сводить стратегию к Нэш-оптимальной
3) Применение чего-то типа Actor-Critic к полученным данным
В результате обучения, алгоритм выдаёт стратегию, занимающую 3 строчку в рейтинге игроков-людей. Учитывая сильно меньшую популярность и изученность Stratego, можно утверждать, что аспект неполной информации очень сильно просаживает способности алгоритма. Однако, результат превосходит все предыдущие, так что, за авторов остаётся лишь порадоваться.
Какое место в реальной жизни занимает такой подход? Замечу, что ни 10^300, ни 10^500, ни 10^5000 не покрывают сколько-нибудь значимой доли реального пространства состояний. Возьмём для сравнения хотя бы Starcraft - даже разделив карту на крупные клетки, каждый из десятков юнитов может быть отправлен в одну из 10000 позиций каждую секунду, тогда как игра может длиться тысячи секунд. 10^100000, уверен, суперконсервативная оценка пространства состояний этой игры.
Но самое смешное в данной ситуации не это. Дело в том, что Нэш-оптимальная стратегия играет в каждую новую игру с чистого листа - она не улучшается с каждой следующей игрой. Она уже оптимальна в том смысле, что её нельзя обыграть - она будет в среднем устойчива к тому, что может быть скрыто от неё. Но она не способна эксплуатировать соперника, используя внешние знания о нём.
Оптимальный бот не сможет быть обыгран, но человек, знающий своих человеческих соперников, будет выигрывать у них чаще, чем оптимальный бот. Чтобы бот смог обогнать человека в выигрыше других людей, ему необходимо уметь переносить весь свой предыдущий опыт в каждую игру и изменять своё поведение со временем. Это звучит так сложно, что, на мой взгляд, только meta-learned алгоритмы, эволюционирующие в среде, населённой человекоподобными стратегиями, сможет этому научиться. Но до этого нам ещё далеко.
@knowledge_accumulator
BY Knowledge Accumulator
Share with your friend now:
tg-me.com/knowledge_accumulator/251
